Confidence intervals provide an estimated range within which we expect a parameter, like a population mean, to fall.
However,In the most-common hypothesis testing, there are common misconceptions about what confidence intervals actually represent, especially when comparing them to the Bayesian approach.
Confidence Intervals are not probability distributions
A common misconception is to interpret confidence intervals as probability distributions, assuming values near the center are more probable than those near the edges.
However, confidence intervals carry no distributional information. They merely define a range of parameter values that would not be rejected by a chosen significance level (often p < 0.05 in a 95% confidence interval). This interval reflects the likely range of a parameter, not a probability spread within the interval.
This interval doesn’t suggest that values near the center are more probable than those near the edges.
The Frequentist Confidence Interval
"Give me an interval where, were the experiment repeated a large number of times, the true value of the statistic would lie within x% of such intervals"
The Frequentist interpretation of a confidence interval answers the question: “If we repeated this experiment many times, what percentage of intervals would contain the true parameter?”
Here, confidence intervals are based on sample distribution and long-run frequencies.
Frequentist statistics treat the parameter as a fixed, unknown value, and repeated samples allow us to estimate a likely range for this fixed parameter.
Importantly, each confidence interval assumes specific sampling and testing conditions—different conditions, like changing sample sizes or adaptive stopping rules, would result in different intervals.
The Bayesian Credible Interval
"Give me an interval where the true value of the statistic lies with x probability",
By contrast, the Bayesian approach interprets intervals as credible intervals that represent the probability of the parameter itself.
Bayesian statistics treat parameters as random variables, combining prior beliefs with new data to update a parameter’s distribution, or “posterior.”
Thus, a Bayesian credible interval might state, “There is a 95% probability that the parameter lies within this interval,” which allows for a direct probability interpretation of the parameter.
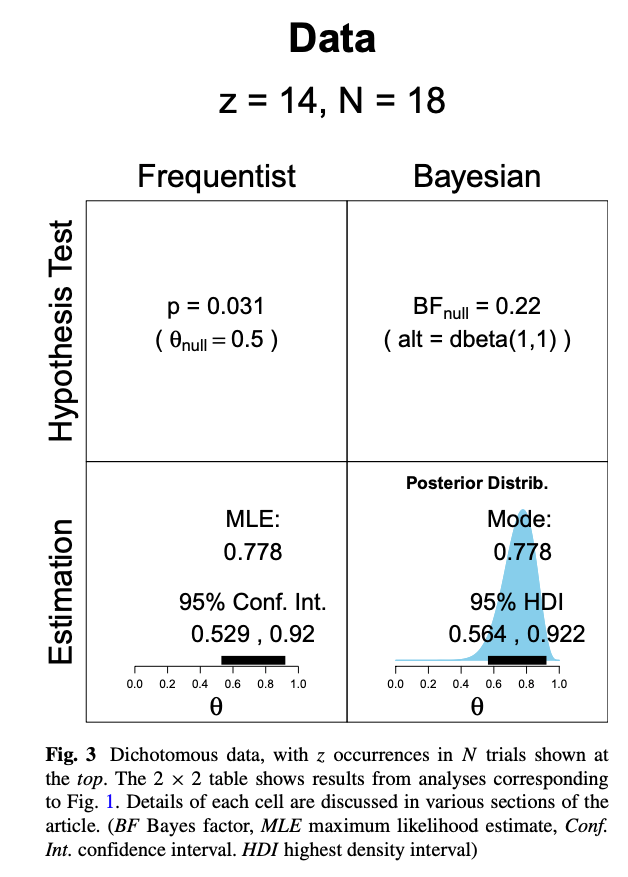
In summary:
- Frequentist confidence intervals offer a range within which the true parameter would fall in repeated sampling but make no probabilistic statements about values within the interval.
- Bayesian credible intervals provide a direct probability statement about the parameter, allowing interpretation as the likelihood of the parameter being within the interval.





